Ketika kebanyakan dari kita melihat mesin taffy-pulling yang sedang berjalan di atas papan jalan turis, kita berpikir tentang gula manis yang manis. Jean-Luc Thiffeault memikirkan matematika yang manis dan manis. Sebagai ahli matematika terapan di University of Wisconsin-Madison, Thiffeault sangat tertarik dengan cara bahan-bahan seperti taffy dicampurkan: Di dalam mesin, permen diregangkan dan dilipat berulang-ulang untuk memasukkan udara dan mengembangkan cahaya, tekstur kenyal. Saat ditarik, persegi panjang asli taffy semakin melebar — panjangnya bertambah secara eksponensial dengan rasio yang sama setiap kali. Rasio peregangan itulah yang menarik minat Thiffeault.
Konten terkait
- Melt-Proof Chocolate, Gummies Dicetak 3D dan Paten Permen Menarik Lainnya
Ketika seseorang menarik gula-gula, umumnya mereka akan mengambil gumpalan permen dan meregangkannya di atas kail, menyatukan kedua ujungnya. Kemudian mereka akan mengambil potongan terlipat itu dan meregangkannya di atas pengait lagi, menggandakan panjangnya, dan seterusnya. Dengan kata lain, "Cara manusia melakukannya adalah faktor multiplikasi dari 2, " kata Thiffeault. Penarik mekanis dapat melakukan lebih baik, seringkali menghasilkan bilangan irasional yang lebih besar dan eksotis sebagai faktor peregangannya.
Ternyata taffy pull dapat dimodelkan oleh bidang abstrak matematika yang dikenal sebagai dinamika topologi, pada dasarnya studi jangka panjang, perubahan skala besar dari waktu ke waktu dalam ruang matematika. (Jika kata topologi terdengar akrab, itu dalam berita baru-baru ini sebagai bagian dari Hadiah Nobel Fisika tahun ini.) Matematika yang sama yang menggambarkan taffy-pulling juga memiliki aplikasi yang lebih serius: banyak proses industri, termasuk peniupan kaca dan persiapan obat, memerlukan cairan kental untuk dicampur dengan cara yang lebih seperti menarik gula-gula dari pada mengaduk krim ke dalam kopi. "Jika Anda mencoba untuk mengaduk hal-hal yang benar-benar kental, seperti pasta industri farmasi, Anda tidak bisa hanya mengguncangnya, " kata Thiffeault. "Ini tidak seperti mencampur cat."
Thiffeault telah memahami taffy-pulling sebagai contoh pencampuran kental untuk waktu yang lama, tetapi hanya baru-baru ini dia benar-benar melihat ke dalam sejarah taffy-puller untuk menggali rahasia matematika mereka. Hasil dari perjalanan ke paten sejarah adalah makalahnya baru-baru ini "Sejarah matematika penarik undi, " diterbitkan pada server preprint arXiv pada bulan Juli.
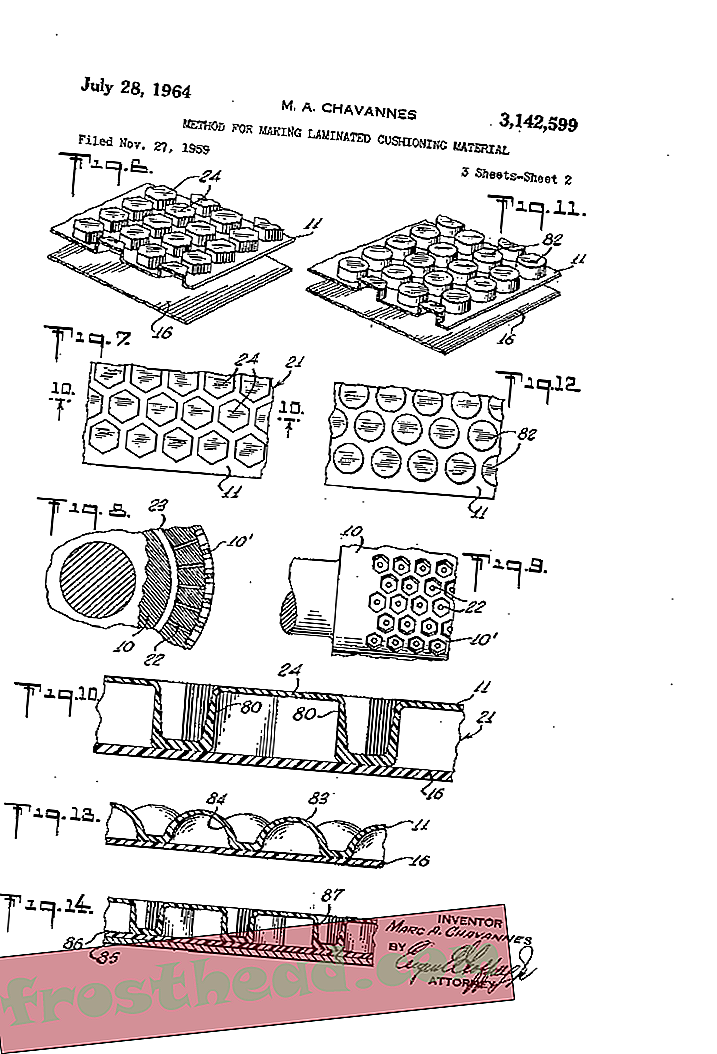
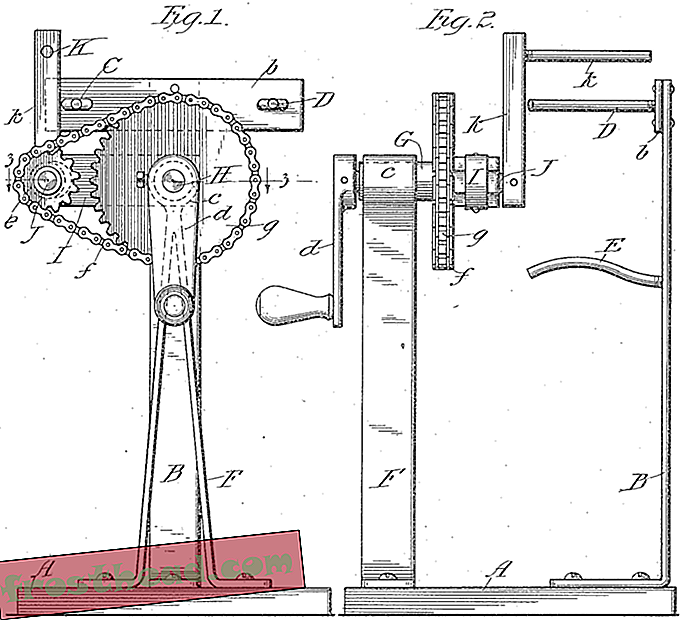Gambar dari paten mesin taffy 1916 yang muncul dalam studi Thiffeault. Secara khusus, daerah yang menyebabkan penyelaman mendalam taffy-puller-nya adalah studi tentang apa yang disebut pemetaan pseudo-Anosov. Pseudo-Anosov adalah cara yang bagus untuk menggambarkan suatu proses di mana bentuk dua dimensi direntangkan secara eksponensial dalam satu arah sementara itu menyusut di yang lain. Secara matematis, studi pemetaan pseudo-Anosov relatif baru. “Di tahun 70-an dan 80-an, orang berusaha sangat keras untuk menemukan contoh, ” kata Thiffeault. Ironisnya, mereka ada di sana selama ini dalam paten untuk taffy-puller. "Karena ahli matematika tidak pernah melihat literatur ini, mereka tidak akan pernah tahu mereka ada, " katanya.
Ketika sedang menyisir paten yang menarik, Thiffeault tersandung pada pertarungan hukum yang berlanjut sampai ke Mahkamah Agung. Yang dipermasalahkan dalam kasus 1921 Hildreth v. Mastoras adalah seberapa luas paten tahun 1900 untuk penarik undi harus ditafsirkan. Yaitu: apakah model kemudian dibuat oleh orang lain hanya perbaikan kecil, atau apakah itu perangkat yang berbeda? Bagian penting dari argumen adalah betapa berbedanya paten 1900 dari pendahulunya tahun 1893 (yang mungkin tidak pernah dibuat). Pendapat pengadilan, yang ditulis oleh Ketua Pengadilan William Howard Taft, "menunjukkan pemahaman yang tajam tentang dinamika topologi, " tulis Thiffeault dalam artikelnya.
Pengadilan mengakui bahwa perangkat sebelumnya - yang hanya memiliki dua kait - tidak dapat memperluas taffy ke tingkat eksponensial yang diperlukan untuk pembuatan konpeksi yang efisien. Pendapat Taft menyatakan:
Dengan hanya dua kait, tidak mungkin ada permen yang menggigit, karena tidak ada pin ketiga untuk menyambungkan kembali permen saat itu dipegang di antara dua pin lainnya. Pergerakan dua pin dalam lingkaran konsentris mungkin akan sedikit merenggangkannya dan mengaduknya, tetapi itu tidak akan menariknya dalam artian.
Thiffeault menulis, "Pendapat Mahkamah Agung menampilkan wawasan mendasar bahwa setidaknya diperlukan tiga batang untuk menghasilkan semacam pertumbuhan yang cepat."
Thiffeault mengatakan ada dua taffy-pullers standar yang digunakan saat ini, satu dengan tiga batang dan satu dengan empat. Mereka kebetulan memiliki faktor peregangan yang sama. Ini terkait dengan apa yang disebut rasio perak, 1+ √2, atau sekitar 2.414, sepupu yang sedikit kurang bercahaya dari rasio emas yang lebih terkenal.
Fakta bahwa dua standar tarik-tarik menarik dengan rasio perak menarik karena rasio perak — dalam pengertian matematika yang tepat — optimal. Namun, Thiffeault memperingatkan bahwa tidak mudah untuk menentukan peringkat taffy-puller yang berbeda, bahkan ketika Anda mengetahui faktor peregangannya: “Ada aspek apel dan jeruk yang cukup sulit untuk dilewati, ” katanya. Satu penarik mungkin memiliki lebih banyak batang dan membutuhkan waktu lebih lama untuk kembali ke kondisi awal daripada yang lain, atau mungkin memerlukan torsi lebih atau lebih rumit. Jadi, meskipun matematika memang memberikan beberapa wawasan tentang seberapa baik taffy-puller menarik, itu tidak menceritakan kisah yang lengkap.
Penelitian Thiffeault mengenai taffy-puller mengilhami dia dan mahasiswa sarjana Alex Flanagan untuk membangun model mereka sendiri. Mereka ingin melihat apakah mereka dapat meningkatkan efisiensi tanpa memodifikasi roda gigi banyak, dan akhirnya membuat penarik 6-batang baru berdasarkan gearing dari penarik 4-batang standar. "Alasan mengapa kami dapat melakukannya adalah karena kami memiliki matematika sekarang, " kata Thiffeault. Mereka dapat memodelkan mesin secara luas di komputer dan memotong banyak percobaan dan kesalahan dengan perangkat fisik nyata yang harus dilakukan oleh penemu. Perangkat 6-batang, yang masih hanya berupa prototipe, membentang taffy sekitar dua kali lipat dari penarik standar di setiap siklus.
Sejauh ini, produsen taffy-puller belum benar-benar mengalahkan pintu Thiffeault untuk mendapatkan sarannya dalam mengoptimalkan desain mereka — Big Taffy tampaknya puas dengan status quo yang meluas — tetapi dia berharap metodenya dapat memiliki efek di industri lain. Selain glassblowing, satu tempat logis untuk optimalisasi pencampuran adalah industri farmasi. Bagaimanapun, mencampurkan vitamin dan obat-obatan membutuhkan kontrol kualitas yang sangat tinggi: Produsen "bersedia membayar banyak uang untuk pencampuran sempurna" karena mereka "tidak dapat mentolerir satu multivitamin buruk dari 1000, " kata Thiffeault. Jadi suatu hari, apoteker mungkin akan memberikan teriakan manis kepada para penarik permen yang setia.
Kemudian lagi, itu mungkin sedikit peregangan.
