Dalam seni atau sastra, mungkin, kecantikan mungkin telah kehilangan mata uangnya dalam beberapa tahun terakhir sebagai standar penilaian atau kriteria untuk keunggulan, dianggap terlalu subjektif atau dimediasi secara budaya. Namun, bagi matematikawan, keindahan sebagai kebenaran abadi tidak pernah ketinggalan zaman. "Kecantikan adalah ujian pertama: tidak ada tempat permanen di dunia ini untuk matematika jelek, " tulis ahli teori bilangan Inggris Godfrey Hardy pada tahun 1941.

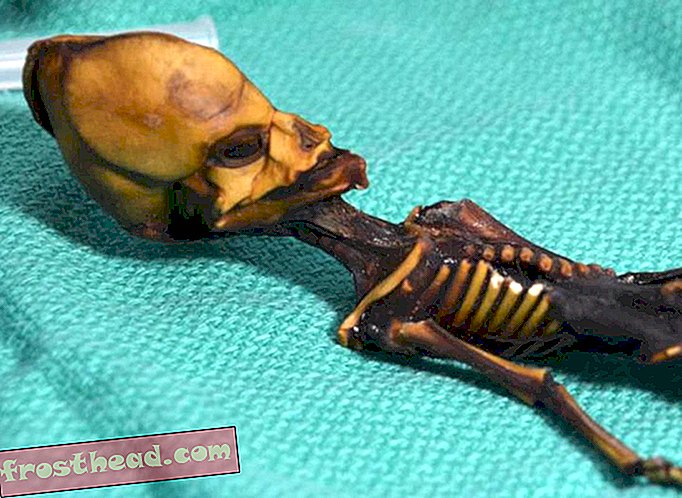
Untuk merasakan keindahan matematika, mulailah dengan pergi ke pub favorit Anda dan memesan segelas bir dingin. Letakkan di atas alas kertas tiga kali, membentuk tiga cincin kondensasi — pastikan untuk melakukannya sedemikian rupa sehingga ketiga cincin berpotongan pada satu titik. Sekarang tanyakan kepada teman Anda: Berapa besar cangkir yang dibutuhkan seseorang untuk menutupi tiga titik persimpangan lainnya? Seseorang hampir selalu berasumsi bahwa hanya mug raksasa yang akan melayani tujuan itu. Jawaban yang mengejutkan: cangkir yang sama! Ini solusi yang sangat mudah. (Lihat gambar di kiri untuk dua solusi yang sama-sama valid; dalam setiap kasus, lingkaran padat adalah tiga cincin pertama; lingkaran putus-putus adalah cincin keempat, mewakili cangkir yang menutupi tiga titik persimpangan lainnya.)
Teorema ini diterbitkan oleh Roger A. Johnson pada tahun 1916. Teorema lingkaran Johnson menunjukkan dua persyaratan penting untuk keindahan matematika. Pertama, ini mengejutkan. Anda tidak mengharapkan lingkaran berukuran sama muncul lagi dalam solusi. Kedua, ini sederhana. Konsep matematika yang terlibat, lingkaran dan jari-jari, adalah yang mendasar yang telah teruji oleh waktu. Namun, teorema Johnson muncul pendek di departemen kecantikan dalam satu hal yang menonjol. Teorema terbaik juga mendalam, mengandung banyak lapisan makna, dan mengungkapkan lebih banyak ketika Anda belajar lebih banyak tentang mereka.
Fakta matematika apa yang memenuhi standar keindahan yang tinggi ini? Matematikawan Jerman, Stefan Friedl, mendukung Teorema Geometriisasi Grigory Perelman, yang mana buktinya ditetapkan hanya pada tahun 2003. Teorema tersebut, yang menciptakan sensasi dalam dunia ahli matematika, memajukan langkah penting dalam klasifikasi topologi tiga dimensi. spasi. (Anda dapat menganggap ruang-ruang ini sebagai kemungkinan alam semesta alternatif.) "Teorema Geometriisasi, " Friedl avers, "adalah objek keindahan yang menakjubkan."
Dimasukkan ke istilah paling sederhana, itu menyatakan bahwa sebagian besar alam semesta memiliki struktur geometris alami yang berbeda dari yang kita pelajari di sekolah menengah. Alam semesta alternatif ini bukan Euclidean, atau datar. Pertanyaannya berkaitan dengan kelengkungan ruang itu sendiri. Ada berbagai cara untuk menjelaskan apa artinya ini; yang paling tepat secara matematis adalah dengan mengatakan bahwa alam semesta alternatif adalah "hiperbolik, " atau "melengkung negatif, " daripada rata.
Matematikawan baru mulai bergulat dengan implikasinya. Data astrofisika menunjukkan bahwa alam semesta kita datar. Namun di alam semesta alternatif ini, kerataan bukanlah keadaan alami. Menurut teorema Perelman, alam semesta kita yang kelihatannya datar merupakan pengecualian yang mengejutkan.
Alasan lain mengapa teorema tersebut menarik publisitas internasional berkaitan dengan ahli matematika itu sendiri. Pada 2010, Rusia yang tertutup menolak hadiah satu juta dolar untuk terobosannya dari Clay Mathematics Institute di Cambridge, Massachusetts. Jelas, bagi Perelman, keindahan matematika bukanlah sesuatu yang bisa dibeli dan dibayar. Mengubah pemahaman kita tentang alam semesta adalah hadiah yang cukup.